


In figuur 2, de achterzijde ziet u de Sextant afgebeeld.
De voorzijde, figuur is echter interessanter voor dit moment, dit stukje tekst.
De Duitse bank begon met de uitgifte van dit biljet in April-1991.
U ziet een portret van Gauss met links daarvan de Gauss-verdeling, de Klokkromme.
*
Deze Klokkromme komen we als eerste tegen in het door Abraham de Moivre in 1733 uitgegeven werk: 'Approximatio ad summan terminorum binomii(a+b)^n in seriem expansi ; wie heeft het niet onder zijn nacht-kussen liggen ;) ?
.
Abraham de Moivre leefde van 1667 - 1754.
Johann Carl Friedrich Gauss leefde van 1777-1855, en heeft deze 'normale verdeling' grondig bestudeerd, en later werd deze 'normale verdeling' dan ook naar hem vernoemd; de Gauss -verdeling.
De Gauss -verdeling beschrijft een belangrijke continue kansverdeling die toepasbaar is op zeer veel gebieden, en we vinden de Gauss -verdeling dan ook vandaag de dag terug in de statistiek.
In de achttiende eeuw ontdekten de wiskundigen al dat een groot aantal metingen op een bepaald gegeven veelal een soortgelijke vorm lieten zien in de grafiek als deze Gauss -verdeling.
Bij het werken met de Gauss -verdeling krijgen we te maken met termen als gemiddelde afwijking en standaard afwijking, deviatie.
Ik kom daar verderop nog op terug.
A. de Moivre gebruikte de 'Normale-verdeling' tijdens zijn studie naar de benadering van de binomiale verdeling, Pierre-Simon Laplace ( 1749-1827) gebruikte deze 'Normale -verdeling voor het bestuderen van meetfouten, en Gauss paste de verdeling onder andere toe bij het bestuderen van Astronomische data.
.
Een mooi kort eenvoudig voorbeeldje voor het werken met zo'n kromme komen we bijvoorbeeld tegen op www.wisfaq.nl bij een vraag van Esther dd. 25-04-2007.
Er wordt gevraagd de normale verdeling volgens de standaard regels te berekenen voor 750 potten jam met een gemiddeld gewicht van 460 gram, en een standaard afwijking van 8 gram.
De vraag iets anders gesteld is: om via de normale -verdeling, dus volgens de Klokkromme te berekenen /weer te geven hoe de verwachting is dat de inhoud van de jampotten uiteindelijk zal zijn.
De berekening is op dit moment voor dit stukje niet van belang, echter wel de bell-curve of klokkromme die daaruit rolt:
Figuur 3:
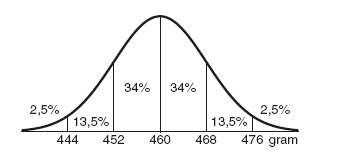
U ziet dat het meeste aantal potten jam van de 750 stuks een inhoud heeft van 460 gram.
De potten die de afwijking plus of min van 8 gram ( de Standaars Deviatie SD ) hebben zal lager liggen, en deze vallen dan nog onder de 'standaard deviatie' en een nog kleiner aantal zal vallen buiten de standaard deviatie.
Nu is figuur drie een zogenaamde 'ideale - situatie', in de praktijk zal de curve afwijken zoals we straks zullen gaan zien.
*
In het stukje: De Cirkel leest u nog wat meer over deze ' klok-kromme ' en hoe je die onder andere terug vindt in het koersverloop, vandaag breid ik dat een stukje uit.
***
**
*
Het volgende stukje komt uit mijn update van 12-December-2009, ik plaats het voor nu belangrijkste stuk daarvan even:
-->
Laten we dit weekend even iets aanroeren wat veel mensen 'links' laten liggen --> Market Profile.
Wanneer u nu even de horizontale as niet als tijd-as ziet, maar als koers-waarde-as, dan kunt u zich indenken dat volgens deze techniek de meeste koersbeweging, in een bepaald tijdframe, zich moet bevinden in het gebied 'same as others', hierboven genoemd de 'Value Area'.
Een kleiner gedeelte van de koersbeweging zal zich bevinden in het gebied 'probably more then others' of 'Probably less than others'.
En een nog kleiner gedeelte daar buiten ... in een ideale markt situatie !
.
Nu worden koersen altijd op een verticale as weergegeven.
We moeten bovenstaande Bell curve dan ook een kwart slag draaien.
.
Grafiek 2:
Grafiek 4 is een Market-profile grafiek over een willekeurig aantal dagen, in dit geval vanaf midden Oktober t/m 12-December-2009.
*<--
Tot zover even uit de Update van 12-December-2009.
*
Wie nog even de laatste grafiek 4 bekijkt en deze vergelijkt met de Bell-curve op zijn kant, kan er toch haast niet omheen dat 'Market Profile' en de 'Bell curve'/ 'Gauss -verdeling' met elkaar te maken hebben.
Het is dan wel geen perfecte Gauss -verdeling, maar die Gauss -curve zal dan in de praktijk ook niet altijd overeenkomen met het ideale beeld.
**
Even een kort uitstapje ...
Wanneer u naar grafiek -4 uit de update van December 2009 hierboven kijkt moet u toch haast het MurreyMath frame ofwel de achtste verdeling van Gann door het hoofd schieten.
Ik heb even een tekenig gemaakt om te laten zien wat ik bedoel.
Figuur 4:
In figuur 4 ziet u de Market-Profile van de AEX-index voor de laatste week van October-2009 tot en met de derde week van December-2009 via de daggrafiek.
Rechts ernaast heb ik even het Basis-MurreyMath frame getekend ofwel de achtste verdeling van Gann.
De horizontale blauwe 4/8 = 50% is zoals u ziet een belangrijk niveau, het is de geÔdealiseerde top van de Bell-curve.
Let ook eens op het rode 2/8 en 6/8 niveau, u herkent de afbakening van 'The Value Area' in de Market-Profile.
Let ook eens op de gele 1/8 lijn, in MurreyMath terminologie 'the fast pivot line'.
Mooie stof voor een volgend stukje.
**
*
Okť Jan, waarom deze paar inleidende regeltjes, wat wil je vertellen ?
Tja, ik wilde er eerst een groot aantal grafieken tegenaan gooien, maar ik denk ik het met een paar woordjes ook wel af kan ;)
Kijkt u nog eens naar grafiek -3 hierboven.
Ik plaats die nog even voor uw gemak hieronder:
Grafiek 3:
Het is een dertig minuten grafiek.
Wat u ziet is dat de tweede curve ligt omhoog verschuift ten opzichte van de eerste, en de derde curve ligt zelfs boven de eerste en de tweede curve.
Met boerenverstand geredeneerd : de trend is omhoog in dat stukje grafiek ! ;)
Het weergeven van het koersverloop door middel van "Market Profile" verschaft ons een blik onder de motorkap van het koersverloop.
Een andere wijze van kijken onder de motorkap van het koersverloop vindt u in het stukje: Onder de Motorkap
Aan het opschuiven van de Bell-curve kunnen we dus zien hoe de trend zich waarschijnlijk gaat ontwikkelen.
Wanneer we de tijd -as in een koersgrafiek zouden uitzoomen zal bij:
-> een zijwaartse trend de verschillende Bell-curves elkaar overlappen,
-> een stijgende trend de verschillende Bell-curves omhoog gaan en een soort van stijgend kanaal vormen,
-> een dalende trend de verschillende Bell-curves omlaag gaan en een soort van dalend kanaal vormen.
Conclusie:
Kort door de bocht zou je kunnen redeneren dat zolang de Bell-curves elkaar overlappen dat de trend zijwaarts is en zodra de Bell-curves elkaar niet meer overlappen dat de trend stijgend of dalend is.
Dit zou een duidelijke manier van trendweergave kunnen zijn.
Dit gaat in principe op voor elk mogelijk tijdframe.
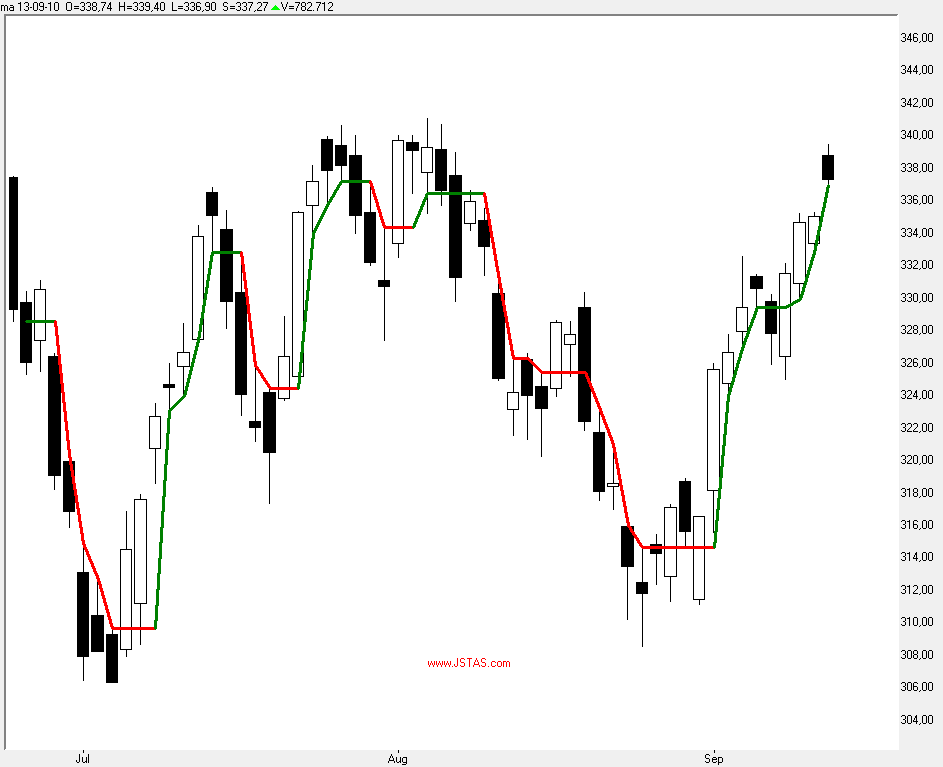
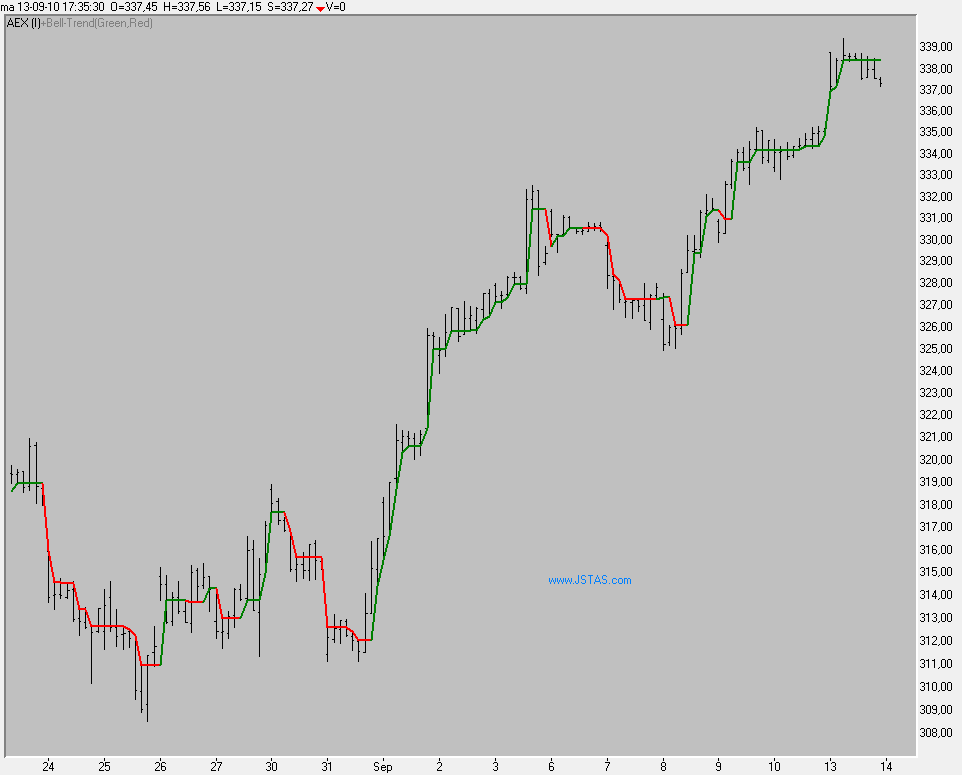
Laten we eens een eenvoudige indicator maken die de trend aan geeft, groen voor een stijgende trend en rood voor een dalende trend, ( ik weet 't --> oersaai ...;-)) waarbij we er vanuit gaan dat de trend stijgend is zodra de Bell-curve omhoog niet meer de voorgaande overlapt en de trend omlaag is zodra de Bell-curve omlaag niet meer de voorgaande Bell-Curve overlapt.
Dit is een zeer grove benadering waarop diverse verfijningen mogelijk zijn, mooi onderwerp voor een vervolg stukje, maar het gaat hier om het basis idee.
Ik heb daarom even een kort stukje software code geschreven die een rode lijn plaats wanneer de trend dalend en een groen lijn plaats wanneer de trend stijgend is volgens bovenstaand idee.
U bent natuurlijk slim, en u handelt daarom niet alleen op het volgende idee, ik wil het alleen even als basis meegeven.
Ik geef u hieronder even de grafiek van een dergelijke benadering op basis van EOD -koersen en Intraday koersen op basis van een uur.
Figuur 5:
Daggrafiek
Figuur 6:
Uurgrafiek
Ach, 't is leuk .. niet dan ;)
.
TA-code vindt u in de Gann topic via de link: TA-script.com -Gann
*
Vriendelijke groet,
JanS ;)
.
Gelezen literatuur:
Tekst van Dhr. H.J. Geels,
Tekst van Dhr. Richard Johnson
Tekst van Dhr. Ron Black.
*