Fibonacci ~~ net iets anders.
- Terug naar hoofdmenu
- De Fibonacci getallen, iedereen kent ze wel, maar ik
zet ze toch nog even op een rijtje.
- Dan laat ik in dit stukje even zien wat "prijs
correcties (retracements) " en "prijs -projecties" zijn, en
dat je die op meerdere manieren kunt toepassen.
- En daarna laat ik een en ander even zien in de
grafieken van alledag, en ook laat ik daarin zien dat de Fibonacci getallen
af en toe op een iets andere wijze moeten worden toegepast.
- *
- Fibonacci en de getallen daarmee berekend:
- De Fibonacci reeks is een reeks die eigenlijk is
"opgesteld en uitgedokterd" door Pythagoras, en later herontdekt
door Leonardo Fibonacci da Pisa, maar ook Pythagoras was niet de eerste ....
- .
- De reeks loopt als volgt:
1,1,2,3,5,8,13,21,34,55,89,144 en zo verder, waarbij het volgende getal in
de reeks is opgebouwd uit de som van de twee voorgaande getallen.
- Wat opvalt bij deze getallen is dat twee opeen
volgende getallen door elkaar gedeeld steeds dezelfde waarde opleveren,
namelijk 0,618 --> bijvoorbeeld 34/55--> 0,618
of 89/144 --> 0,618
- Dit werkt ook andersom: 55/34 -->
1,618 of 144/89 --> 1,618 en zo verder
- Zo zijn er meerdere waarden uit te halen door iets
andere waarden uit de reeks op elkaar te delen.
- 34/144 --> 0,236
- 55/144 --> 0,382
- 89/144 --> 0,618
- Allemaal keurige Fibonacci waarden.
- In de technische analyse zie je dat vaak ook nog
gebruik gemaakt wordt van het getal 0,5 wat ik echter eerder terug
vindt bij Gann, ik vind dat geen Fibonacci getal.
- Ook kom je vaak het getal 0,786 tegen, en wie
een rekenmachine bij de hand heeft ziet direct dat dit getal de wortel is
uit het Fibonacci getal 0,618
- *
- Spelen we even verder met deze getallen, en laten we
dan beginnen bij 1.
- 1 X (1+0,236) --> 1,236
- 1 X (1+0,382) --> 1,382
- 1 X (1+0,500) --> 1,5
- 1 X (1+0,618) --> 1,618
- En om daarna niet teveel lijnen in de grafiek te
krijgen nemen we voor de volgende getallen gewoon het getal 1,618 steeds
vermenigvuldigd met 1,618:
- 1,618 X 1,618 --> 2,618
- 2,618 X 1,618 --> 4,236
- 4,236 X 1,618 --> 6,85
- .
- Ik heb voor mijzelf daar nog de waarde 2 aan
toegevoegd.
- .
- Dit geeft dan het volgende rijtje getallen:
- 0,236 -- 0,382 - 0,500 -- 0,618 -- 0,786 -- 1 --
1,236 -- 1,382 -- 1,5 -- 1,618 -- 2 -- 2,618 -- 4,236 -- 6,85
- .
- In de praktijk zie je dat sommige getallen vaker
voor komen dan andere getallen.
- .
- Retracements:
- In de technische analyse duiden we met het woord
retracement een reactie aan van het koersverloop op de er aan
voorafgaande koersbeweging, waarbij we er dan vaak ook nog vanuit gaan, dat
de retracement een correctie is op de trend
- Een voorbeeld:
- De koers van aandeel X is gestegen van 100 naar 110
en de indicatoren geven aan dat de stijging waarschijnlijk even stopt en dat
er winst genomen gaat worden.
- Omdat verwacht wordt dat daarna de koers weer verder
gaat stijgen ( (omdat bijvoorbeeld de Elliott -analyse techniek daarna nog
een koersverloop in dezelfde richting als het koersverloop van 100
--> 110 verwacht ) gaan we er in eerste instantie van uit dat niet de
volledige stijging van 100 --> 110 zal verdwijnen, maar slechts een
gedeelte ervan --> door winstnemingen zal slechts een gedeelte van de
koersstijging worden gecorrigeerd.
- Bijvoorbeeld volgens de Fibonacci getallen
0,382 -- 0,618 of het getal 0,5 --> 38,2
% 50% of 61,8%
- Valt dan de koers terug naar 103,82 waarna deze weer
verder stijgt, dan zegt men: de koersbeweging heeft een retracement gemaakt
van 61,8%.
- .
- Een vaak voorkomende denkfout is het idee dat de
koers geen groter retracement kan maken dan 100%
- Uitzonderingen bevestigen de regel, en een
golfbeweging waarin dit regelmatig voorkomt (retracement groter dan 100%) is
bijvoorbeeld in een correctiegolf welke een flat -correctie wordt genoemd in
de Elliott analyse techniek.
- In een flat correctie golf komt het regelmatig voor
dat de B golf meer dan 100% corrigeert op de A golf.
- Hiervan is een voorbeeld te zien in grafiek 2.
- .
- Het is dus noodzaak er goed op te letten in welk
gedeelte van het koersverloop je welk retracement toepast en gebruikt.
- .
- Prijs projecties:
- De Fibonacci getallen kunnen ook worden toegepast om
koersdoel projecties te maken voor het koersbereik van de golf na een
retracement.
- Dit bekijken we dan altijd in de richting van de
golf waaruit deze berekend wordt.
- Een voorbeeld:
- De koers van aandeel X stijgt van 100 -> 110 en
de Elliott analyse geeft aan dat dit waarschijnlijk golf 1 is van een
grotere beweging.
- Na deze golf 1 volgt een correctie door middel van
een retracement van 50% en de koers staat dan op 105 waar einde golf 2
staat.
- Om dan in eerste instantie koersdoelen uit te kunnen
zetten voor de golf 3 gaan we doelen berekenen aan de hand van de lengte van
golf 1 welke 10 punten is in dit voorbeeld.
- We nemen dan bijvoorbeeld getallen uit het rijtje
1,382 -- 1,500 -- 1,618
- Dat levert de waarden 13,8 -- 15 -- 16,2 op.
- Koersdoelen worden dan 118,8 -- 120 -- 121,2
- .
- Genoeg theorie, we kijken even hoe dit in de
praktijk werkt, waarbij er dan iets op zal gaan vallen bij grotere
bewegingen.
- .
- Grafieken:
- *
- Grafiek 1:
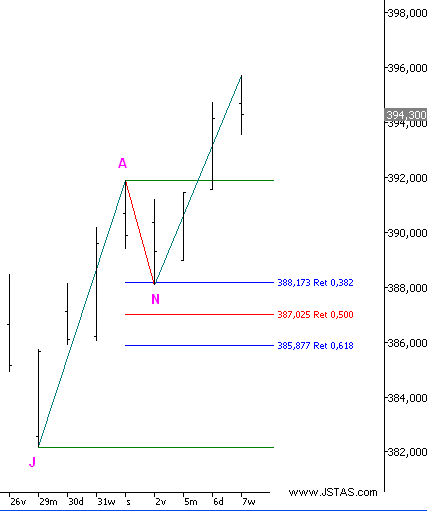
- In grafiek 1 ziet u een voorbeeld van een
retracement.
- De koers stijgt van J naar A, waarna deze een
correctie maakt, een retracement, van 38,2% naar punt N om vervolgens
verder te stijgen.
- *
- Grafiek 2:
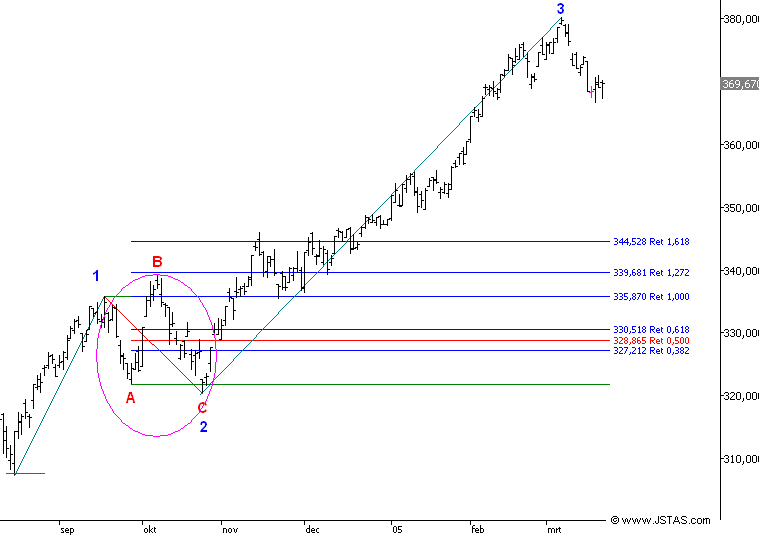
- In grafiek 2 ziet u een impulsgolf 1-2-3 waarbij de
correctiegolf -2 (paarse cirkel) bestaat uit een flat correctiegolf A-B-C
- Duidelijk is te zien dat golf A-B een retracement
maakt op golf 1-A van 127%.
- *
- Grafiek 3:
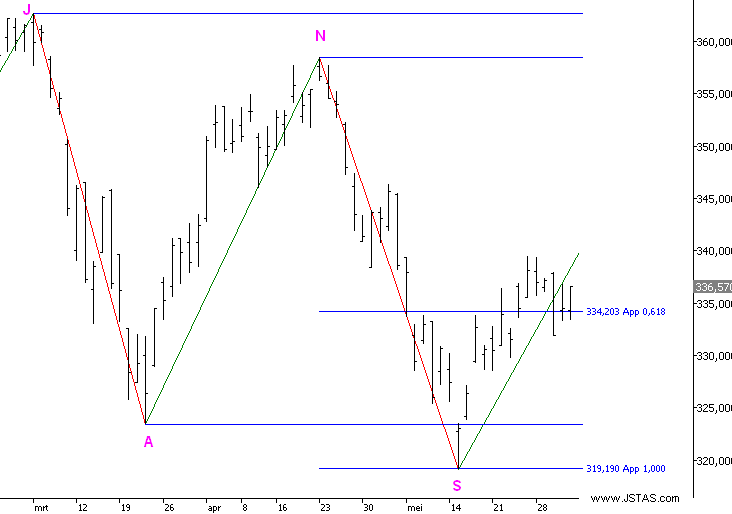
- In grafiek 3 ziet een mogelijkheid van koers-doel
projectie.
- De koers daalt van J naar A, en plaatst vervolgens
een retracement naar N.
- We nemen nu de lengte van golf J-A, en zetten
koersdoel lijntjes uit op 61,8% - 100% 123,6%
enzovoorts vanuit punt N naar beneden.
- De verkregen waarden zijn dan onder andere 334,2 bij
61,8% en 319,19 bij 100%
- De koers stopte keurig bij 100%
- *
- Laten we eens kijken of dit altijd opgaat, en dan
vooral bij grote koers bereiken.
- *
- Grafiek 4:
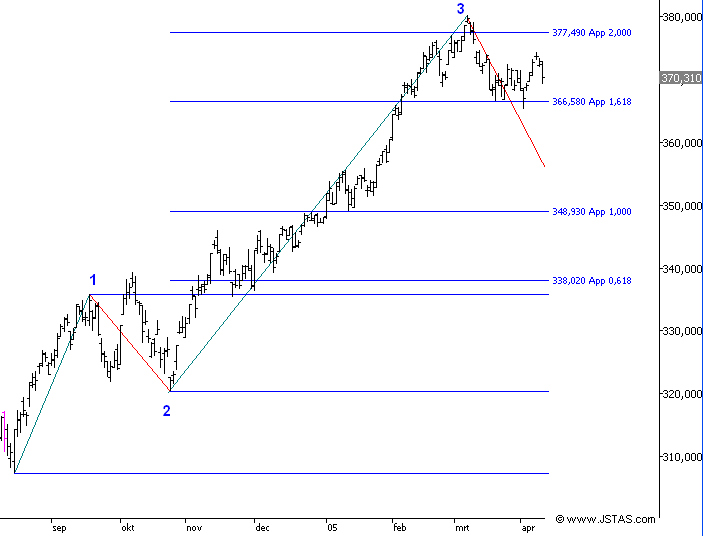
- In grafiek 4 zien we een groot koersbereik van golf
3 van ongeveer 60 punten.
- De koersdoel projecties zijn uitgezet vanaf einde
golf 2 en zijn berekend uit de lengte van golf 1.
- We zien dat de top van golf 3 een paar punten wordt
gemaakt voorbij de koersdoel projectie van 200%.
- Top golf 3 was 380,19 en de 200% koersdoel
projectie ligt op 377,49.
- *
- Kan dit nauwkeuriger ? ---> Ja, dat
kan ;-))
- En wel door de Fibonacci waarden iets anders te
berekenen:
- Golf 1 startte op een koerswaarde van 307,31 en
eindigde op een koerswaarde van 335,87
- Dat is een stijging van (335,87 - 307,31)/307,31
--> 9,2935%
- Golf 3 startte op een koerswaarde van 320,37.
- De koersdoel projectie wordt dan deze keer berekend
door de getallen uit het rijtje toe te passen op het percentage stijging
--> 1,618 x 9,2935% of 2 x 9,2935% wat de waarden 15,0367% en
18,587% oplevert.
- 15,0367% van 320,37 --> 48,17
en 18,587% van 320,37 --> 59,54
- De koersdoel projectie waarden zijn dan 320,37 +
48,17 --> 368,54 en 320,37 + 59,54 --> 379,91
- Dit ziet er in de grafiek als volgt uit.
- Grafiek 5:
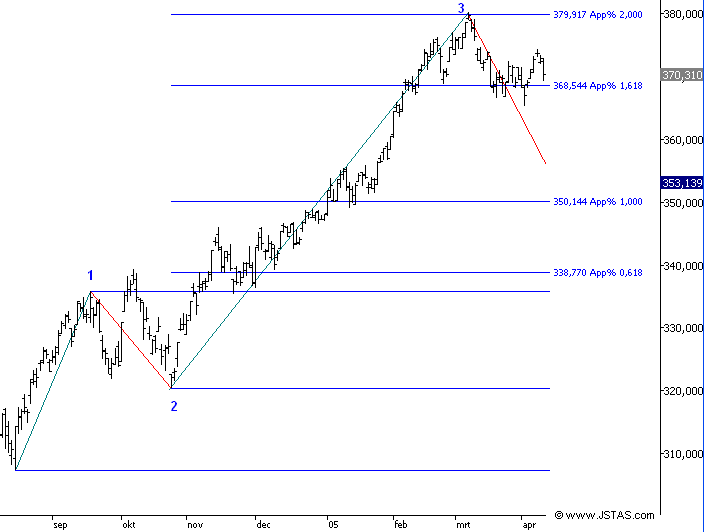
- Duidelijk is te zien dat de top in de grafiek beter
ligt bij de berekende waarde dan in grafiek 4.
- *
- *
- Nog een voorbeeldje, maar dan van een retracement.
- Grafiek 6:
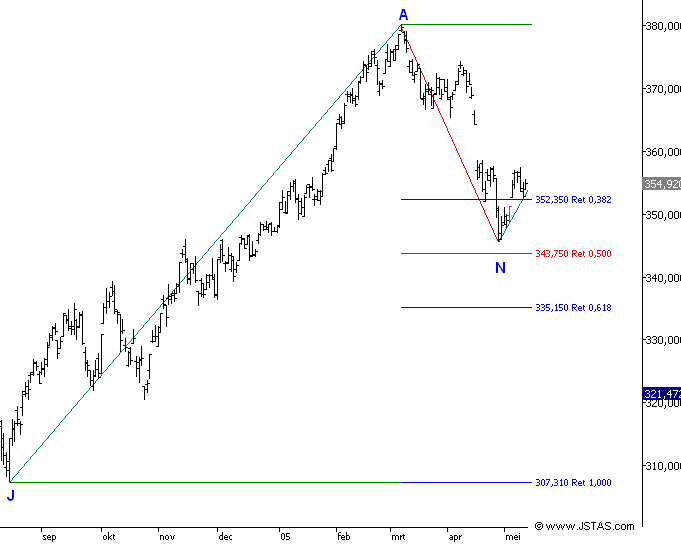
- In grafiek 6 ziet een retracement golf A-N als
correctie op de stijgingsgolf J-A
- De koers welke bij N geplaatst werd had de waarde
345,55.
- Dit was meer dan de waarde welke staat bij 38,2%
maar minder dan de waarde welke staat bij 50%
- .
- Laten we dit nu ook eens procentueel bekijken.
- Stijging van J naar A was 380,19 - 307,31 -->
72,88 punten -/- 23,715%
- Dan rekenen we retracement percentages uit:
- 38,2% van 23,715% --> 9,059%
en 50% van 23,715% --> 11,8575%
- 380,19 - 9,05% --> 345,75 en 380,19 -
11,8575% = 335,1
- Dit ziet er dan in de grafiek als volgt uit:
- Grafiek 7:
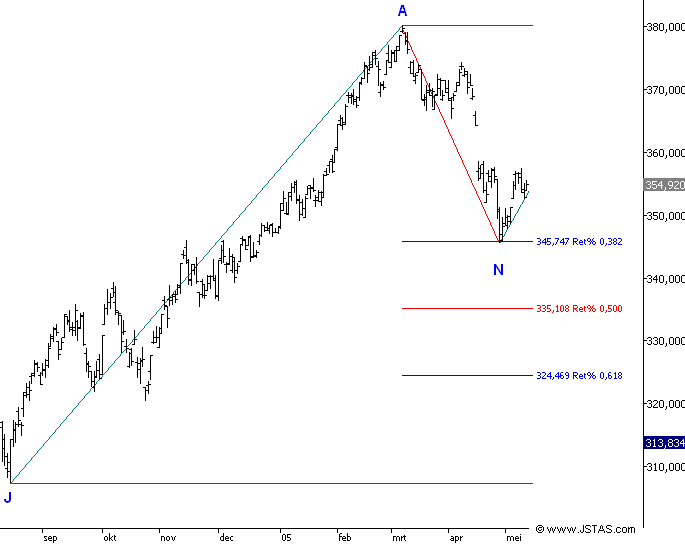
- U ziet dat de Fibonacci getallen losgelaten op het
percentage stijging of het percentage daling beter werken dan dat u de
Fibonacci getallen rechtstreeks toepast op het koersverschil.
- Een beetje hetzelfde geval als in het artikeltje
"de juiste lijn".
- .
- Moet u nu in het vervolg overgaan op alleen maar
procentuele berekeningen?
- Nee, maar houdt ze wel in het achterhoofd, zeker als
de koersbewegingen wat langer worden.
- .
- Groet, Jan.
-
- email: Jan@Jstas.com
- Terug naar hoofdmenu
Disclaimer:
Bovenstaande zijn slechts ideeŽn, verwachtingen en hersenspinsels. Ze hoeven
dan ook helemaal niet te kloppen met de werkelijkheid. Handelen met deze
gegevens op de beurs is derhalve voor eigen risico, en wordt afgeraden. U kunt
daarbij al uw geld verliezen, en meer dan dat !!